백준/25682번/체스판 다시 칠하기2/골드5

Problem Link: https://www.acmicpc.net/problem/25682

문제 설명

Site: Baekjoon
Number: 25682
Category: 누적 합
Rank: Gold 5

기존에 브루트포스로 해결하였던 체스판 다시 칠하기 문제를 새로운 조건을 통해 누적 합으로 계산하는 문제로 바뀌었다.

주어진 배열의 K x K만큼 잘라내어 체스판으로 만들 때 칠해야 하는 칸의 최소 값을 구하는 문제이다.

2차원 누적 합을 계산하기 위해 입력값을 받고 첫 칸이 검은색인 경우와 하얀색인 경우로 나누어 계산하였다
*하나의 배열로 계산한 후 값을 반대로 뒤집어도 되지만 직관성을 위해 두개로 나누었다. (메모리 사용량 증가)

첫 칸이 검은색인 경우와 하얀색인 경우에 따라 바뀌어야 하는 칸은 1로 표시를 한 후, 오른쪽으로 한 번 아래로 한 번 누적 합을 진행하여 2차원 누적 합 배열을 만든다.

이 후 K x K만큼 자른 값의 체스판을 만들기 위한 최소 값을 계산하기 위해 K-1,K-1좌표에서 시작하며 모든 좌표를 돌며 아래와 같은 경우에 따라 계산한다.

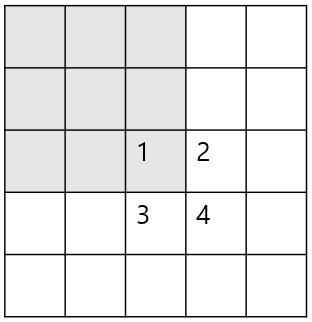
1. 좌표가 K-1, K-1인 경우

이 경우 1에 있는 값이 K x K칸을 체스판으로 만들기 위한 최소 값이기 때문에 1의 값을 그대로 가져다 쓰면 된다.

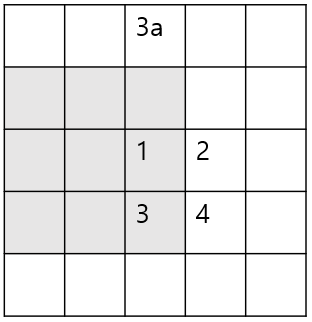
2. 좌표 중 하나만 K-1인 경우

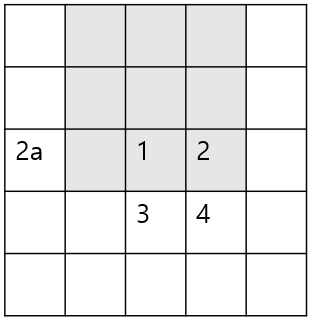
2와 3이 이에 해당한다. 이 경우 해당 칸에 있는 값은 K x K에 포함되어 있지 않은 그 전 값도 포함되어 있기 때문에 2번의 경우 2a의 값을, 3번의 경우 3a의 값을 빼주어야한다.

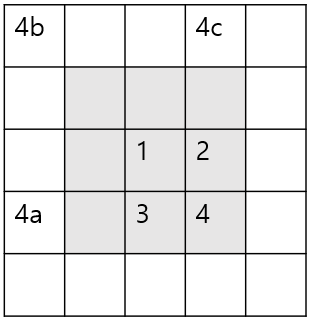
3. 좌표 모두 K-1이 아닌 경우

3번은 4번 칸의 경우로 이 경우 2와 3처럼 중복된 값을 빼주기 위해 4a와 4c를 뺀다면 4b의 값이 중복으로 빠지기 때문에 추가로 4b를 더해준다면 4의 K x K칸 만들기에 필요한 값을 구할 수 있다.

#include <iostream>

using namespace std;

enum
{
	BLACK, WHITE
};

int white[2000][2000];
int black[2000][2000];
int chess[2000][2000];

int main()
{
	ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);

	int N, M, K;
	cin >> N >> M >> K;

	for(int i = 0; i < N; i++)
	{
		for(int j = 0; j < M; j++)
		{
			char c;
			cin >> c;

			switch(c)
			{
			case 'B':
				chess[i][j] = BLACK;
				break;
			case 'W':
				chess[i][j] = WHITE;
			}

			if(i % 2 == j % 2)
			{
				if (chess[i][j] == BLACK)
					white[i][j]++;
				else
					black[i][j]++;
			}
			else
			{
				if (chess[i][j] == BLACK)
					black[i][j]++;
				else
					white[i][j]++;
			}
		}
	}

	for(int i = 0; i < N; i++)
	{
		for(int j = 1; j < M; j++)
		{
			white[i][j] += white[i][j - 1];
			black[i][j] += black[i][j - 1];
		}
	}

	for (int i = 1; i < N; i++)
	{
		for (int j = 0; j < M; j++)
		{
			white[i][j] += white[i - 1][j];
			black[i][j] += black[i-1][j];
		}
	}

	int ans = 2147483647;

	for(int i = K-1; i < N; i++)
	{
		for(int j = K-1; j < M; j++)
		{
			if (i - K+1 > 0 && j - K+1 > 0)
				ans = min(min(ans, white[i][j] + white[i - K][j - K] - white[i - K][j] - white[i][j - K]), black[i][j] + black[i - K][j - K] - black[i - K][j] - black[i][j - K]);
			else if (i - K+1 == 0 && j - K+1 == 0)
				ans = min(min(ans, white[i][j]), black[i][j]);
			else if (i - K+1 == 0)
				ans = min(min(ans, white[i][j] - white[i][j - K]), black[i][j] - black[i][j - K]);
			else if (j - K+1 == 0)
				ans = min(min(ans, white[i][j] - white[i-K][j]), black[i][j] - black[i-K][j]);
		}
	}

	cout << ans;

	return 0;
}