백준/2240번/자두나무/골드5

Problem Link: https://www.acmicpc.net/problem/2240

문제 설명

Site: Baekjoon
Number: 2240
Category: Dynamic Programming
Rank: Gold 5

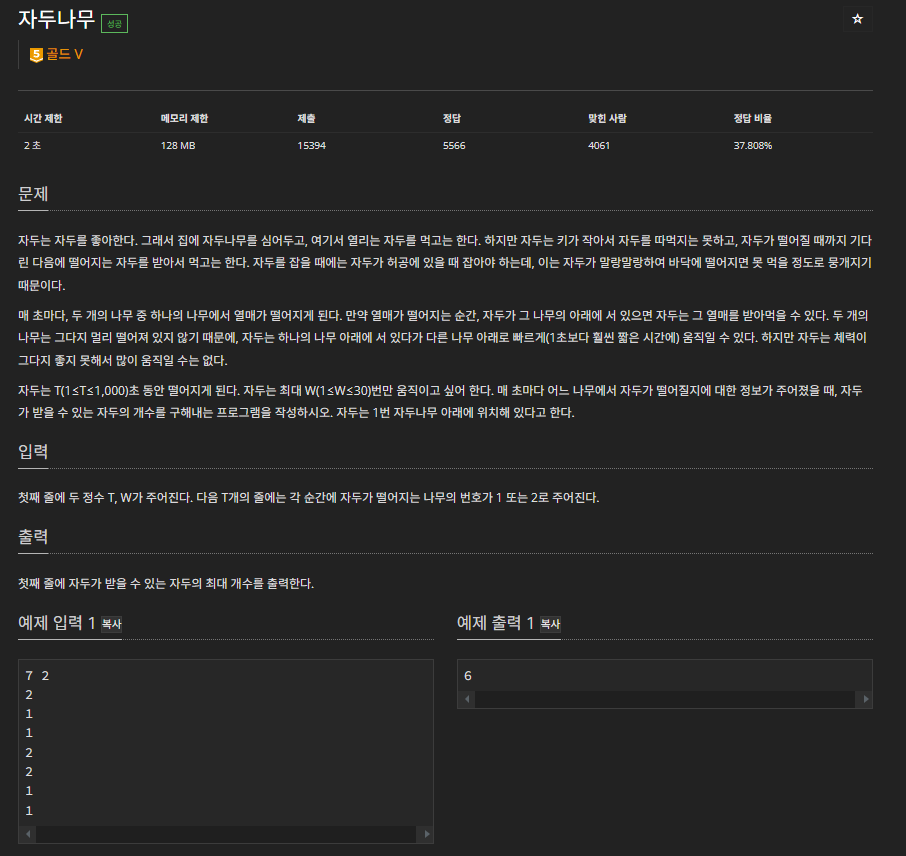
1번과 2번 두개의 나무가 있고 1번 나무에서 시작하여 제한된 수 만큼 움직일 수 있을 때 양쪽 나무에 떨어지는 자두를 먹을 수 있는 최댓값을 구하는 문제입니다.

많은 이전 데이터가 필요한 DP문제로, N번 만큼 움직였을 때 먹을 수 있는 자두 수의 최댓값을 저장하여야 함으로 3차원 배열에 DP값을 저장해야 해결할 수 있습니다.

풀이 과정

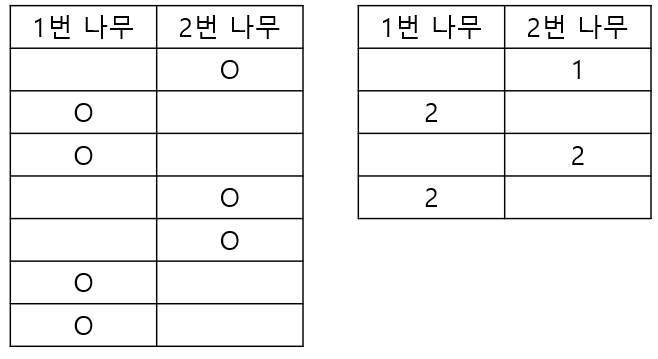
1. 입력 받은 자두를 다음과 같이 정렬합니다. (움직이지 않고 한번에 먹을 수 있는 최대양으로 정렬)

2. [W][T][2] 배열을 선언합니다. 이 배열은 1번 또는 2번 나무에서 [W]만큼 움직였을 때 [T]시간때에 먹을 수 있는 최댓값을 의미합니다.

3. N번 움직였을 때 각 나무에서의 최댓값을 다음과 같은 점화식으로 갱신합니다.

   N번 움직였을 때 한 나무에서의 최댓값은 이전 N번 움직였을 때 한 나무에서의 최댓값과 이전 N-1번 움직였을 때 반대편 나무에서의 최댓값 중 큰 값에 현재 나무에서 먹을 수 있는 자두의 양입니다.
   dp[j][i][0] = max(dp[j][i - 1][0], dp[j - 1][i - 1][1]) + arr[i][0];

   dp[j][i][1] = max(dp[j][i - 1][1], dp[j - 1][i - 1][0]) + arr[i][1];

4. 0~N번 움직였을 때 중 최댓값이 존재할 수 있으므로 그 중 먹은 자두 양의 최댓값을 구하기 위해 매 for문 마다 최댓값은 갱신합니다.

#include <iostream>

using namespace std;

#define PII pair<int, int>

int arr[1001][2];
int dp[31][1001][2];

int main()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    int T, W;
    cin >> T >> W;

    int num, idx = 1;

    cin >> num;

    arr[idx][num-1]++;

    for(int i = 1; i < T; i++)
    {
        int tmp;
        cin >> tmp;

        if (num != tmp)
        {
            num = tmp;
            idx++;
        }

        arr[idx][num-1]++;
    }

    dp[0][0][0] = arr[0][0];
    for(int i = 1; i <= idx; i++)
    {
        dp[0][i][0] = dp[0][i-1][0] + arr[i][0];
    }

    int ans = dp[0][idx][0];

    for(int j = 1; j <= W; j++)
    {
        for (int i = 1; i <= idx; i++)
        {
            dp[j][i][0] = max(dp[j][i - 1][0], dp[j - 1][i - 1][1]) + arr[i][0];
            dp[j][i][1] = max(dp[j][i - 1][1], dp[j - 1][i - 1][0]) + arr[i][1];
        }

        ans = max(ans, max(dp[j][idx][0], dp[j][idx][1]));
    }

    cout << ans;

    return 0;
}