백준/16946번/벽 부수고 이동하기/골드2

Problem Link: https://www.acmicpc.net/problem/16946

문제 설명

Site: Baekjoon
Number: 16946
Category: DFS
Rank: Gold 2

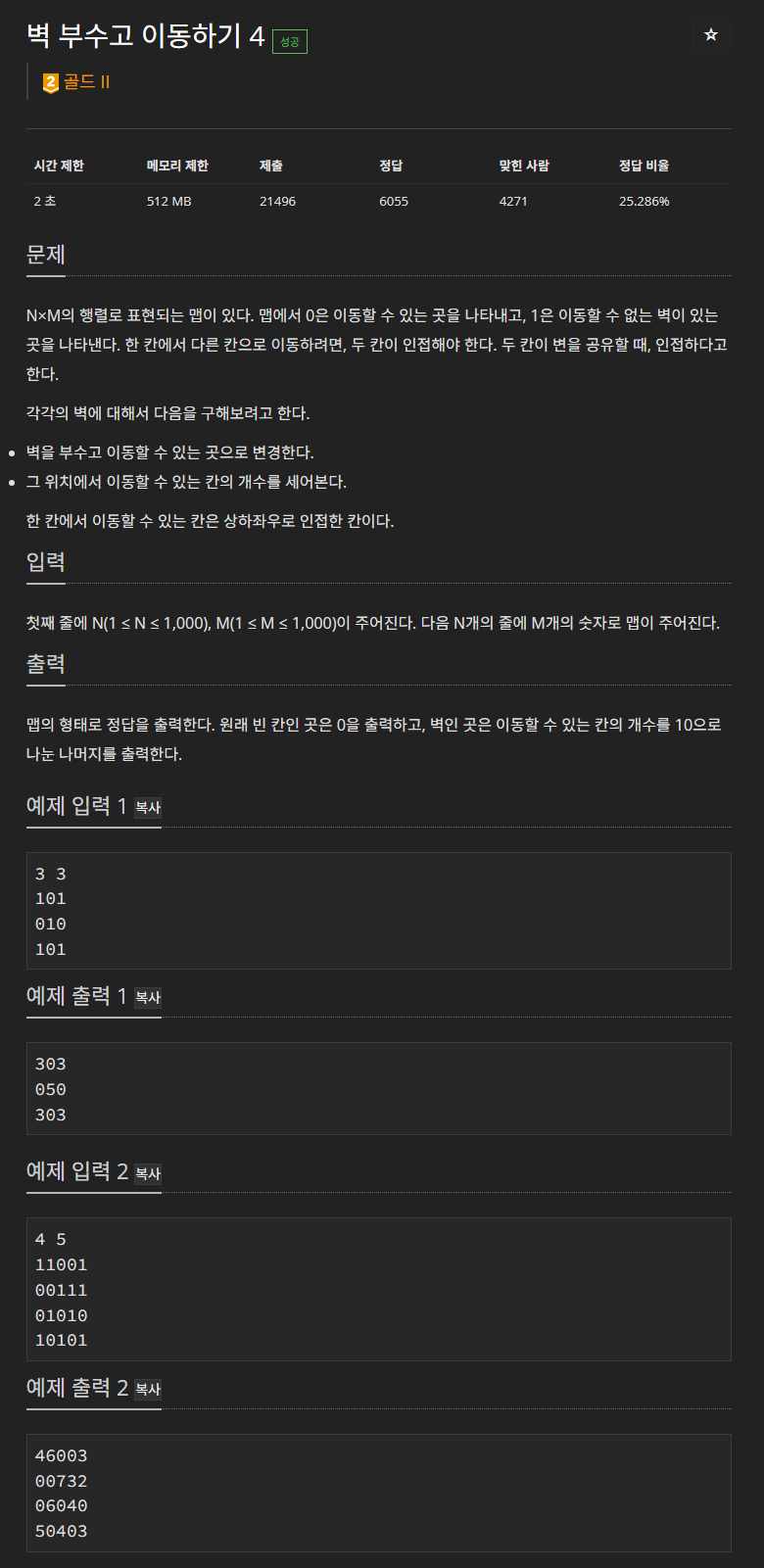
벽이 있는 2차원 공간이 주어졌을 때, 하나의 벽을 없앤 후 지나갈 수 있는 공간의 수를 모든 벽 위치에 출력하는 문제입니다.

문제 풀이

DFS에 queue와 unordered_map을 적용하여 문제를 해결하였습니다.

시도 1
첫 해결 방법은 모든 벽마다 DFS를 진행하여 해당 벽을 없앤 경우 갈 수 있는 모든 공간의 수를 파악하였습니다.

실패: 시간초과

시도 2
시간초과를 해결하기 위해 벽이 아닌 공간을 먼저 파악하고 해당 공간과 연결되어 있는 공간의 수를 세어 이를 dp배열에 저장하고, 벽을 순회하며 옆에 저장된 공간의 갯수들을 가져와 출력하는 방법을 사용했습니다.

실패: 연결되어 있는 공간의 중복 계산

풀이 시도2에서 중복계산을 해결해주기 위해 dp배열의 크기를 3차원으로 변경하였으며, 벽의 공간을 새고 저장하는 과정에서 고유 번호를 통해 추후 합치는 과정에서 unordered_map을 통해 식별할 수 있도록 하였습니다.

#include <iostream>
#include <cstring>
#include <queue>
#include <unordered_map>

#define PII pair<int, int>

using namespace std;

int arr[1001][1001];
int dp[1001][1001][2];
bool visited[1001][1001];

int N, M;

int dirx[4] = { 0, -1, 0, 1 };
int diry[4] = { -1, 0 , 1, 0 };

queue<PII> q;

int DFS(int x, int y, int count)
{
	q.emplace(x, y);
	count++;
	visited[x][y] = true;

	for(int i = 0; i < 4; i++)
	{
		int newx = x + dirx[i];
		int newy = y + diry[i];

		if (newx >= N || newy >= M || newx < 0 || newy < 0 || visited[newx][newy] == true || arr[newx][newy] == -1)
			continue;

		count = DFS(newx, newy, count);
	}

	return count;
}


int main()
{
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    cin >> N >> M;

    for(int i = 0; i < N; i++)
    {
	    for(int j = 0; j < M; j++)
	    {
			char c;
			cin >> c;
			if (c == '1')
				arr[i][j] = -1;
			else
				arr[i][j] = c - 48;
	    }
    }
	int count = 0;
    for(int i = 0; i < N; i++)
    {
	    for(int j = 0; j < M; j++)
	    {
			if (arr[i][j] == 0 && visited[i][j] == false)
			{
				int num = DFS(i, j, 0);

				while(!q.empty())
				{
					PII cur = q.front();
					q.pop();
					dp[cur.first][cur.second][0] = num;
					dp[cur.first][cur.second][1] = count;
				}
				count++;
			}
	    }
    }

	for(int i = 0; i < N; i++)
	{
		for(int j = 0; j < M; j++)
		{
			if (arr[i][j] == 0)
				cout << 0;
			else
			{
				int num = 1;
				unordered_map<int, int> um;

				for(int k = 0; k < 4; k++)
				{
					int newx = i + dirx[k];
					int newy = j + diry[k];

					if (newx >= N || newy >= M || newx < 0 || newy < 0 || arr[newx][newy] == -1 || um[dp[newx][newy][1]] > 0)
						continue;

					num += dp[newx][newy][0];
					um[dp[newx][newy][1]]++;
				}
				cout << num % 10;
			}
		}
		cout << '\n';
	}

    return 0;
}