세그먼트 트리 (Segment Tree)

세그먼트 트리 (Segment Tree)

세그먼트 트리는 구간 내 연산을 빠르게 해줄 수 있게 도와주는 자료 구조 입니다. (구간 합, 최솟값, 최댓값, 평균값)

구조

세그먼트 트리는 이진 트리 구조로 이루어져 있습니다.

구간 합을 위한 세그먼트 트리를 제작한다고 가정할 때, 루트는 모든 노드의 합이며, 자식들을 내려가며 구간 합이 아닌 하나의 노드가 될 때까지 숫자를 갱신합니다.

1~5의 경우를 예로 들면, 루트 노드는 1~5범위의 합이 되며 왼쪽 자식은 1~3범위, 오른쪽 자식은 4~5범위가 되고, 이를 하나의 숫자만 포함할 때 까지 반복하는 것입니다.

1~5의 경우

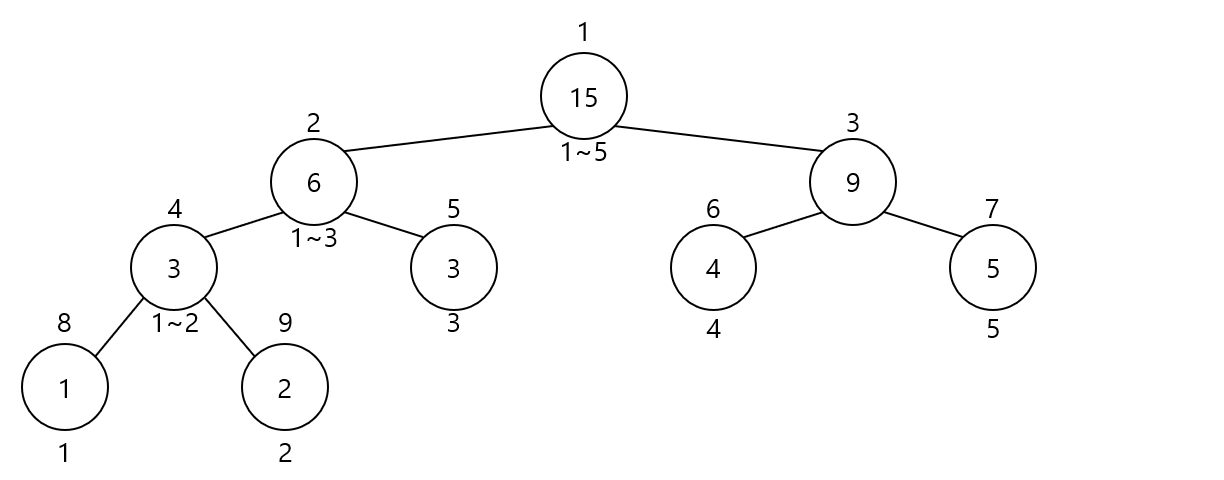
numbers 배열에 1~5를 넣고 다음 코드를 통해 위와 같은 형태를 sum 배열로 구현할 수 있습니다.

void Sum(int idx, int start, int end)
{
    if(start == end)
    {
        sum[idx] = numbers[start];
        return;
    }

    int mid = (end + start) / 2;

    Sum(idx * 2, start, mid);
    Sum(idx * 2 + 1, mid+1, end);

    sum[idx] = sum[idx * 2] + sum[idx * 2 + 1];
}

구간 합

구간 합을 구하는 과정은 루트 노드에서 시작하며 재귀 함수를 통해 구현할 수 있습니다.

1. 현재 노드의 포함 범위가 구간 합을 구해야 하는 범위 밖이라면 return 한다.

2. 현재 노드의 포함 범위가 구간 합을 구해야 하는 범위 안이라면 구간 합에 현재 노드 값을 더하고 return 한다.

3. 그 외의 경우 포함 범위가 밖이거나 안일때 까지 왼쪽 자식과 오른쪽 자식을 탐색한다.

void FindSum(int idx, int start, int end, int left, int right, long long& ans)
{
    if (end < left || start > right)
        return;

    if(left <= start && right >= end)
    {
        ans += sum[idx];
        return;
    }

    int mid = (start + end) / 2;

    FindSum(idx * 2, start, mid, left, right, ans);
    FindSum(idx * 2 + 1, mid+1, end, left, right, ans);
}